In Part 1 of our decision science and football series, we laid some groundwork on decision trees and covered expected value. Moving to roster building scenarios, team builders face uncertainty at every turn. Decision making under uncertainty is a complex process that involves assessing multiple options and potential outcomes in situations where the future is not known. In such scenarios, decision makers often rely on various decision-making approaches to select the best possible option.
There are several common approaches to decision making under uncertainty: maximax, maximin, minimax regret, and an approach that combines the first two (the Hurwicz criterion). In the context of decision theory, regret means the difference (think subtraction) between the outcome of the best possible decision and the decision that was made.
Each approach can be applied to rostering players on offense, defense, and special teams. Each approach also considers different aspects of player potential, enabling general managers and coaches to make informed choices based on their risk tolerance and overall objectives. This is different from the standard expected value approach discussed in Part 1.
Maximax
The maximax (or “maximize the maximum”) approach seeks to maximize the potential gain by selecting the option that offers the highest possible payoff. This approach assumes the best possible outcome and largely ignores any associated risk or downside. For example, when adding players to a roster, the maximax approach would involve selecting players with the highest expected performance, assuming their best possible performance on the field. Selecting individuals with the most significant potential upside (e.g., the best athletes) is consistent with a maximax approach. One risk of a coach taking a maximax approach is that they may select a talented player that is often injured or an unproven player that has displayed historical athletic traits.
On the defensive side of the ball, a maximax coach might opt for a cornerback known to come down with interceptions even while struggling with consistency in coverage. This approach may be appropriate when the team is looking to win at all costs, as the risks associated with selecting these players are deemed acceptable. Decision makers using this approach are often considered to be risk-seeking. While attractive, this approach is not without its drawbacks. There are often constraints (like the NFL salary cap) that limit its full implementation.
Here is a simplified illustration of the maximax approach: A team is considering drafting a generational-level talent (GT) running back. At the time of the draft, it is not known whether the player will turn out to be Offensive Rookie of the Year (OROY), a solid contributor, or off the roster within a few years. Each of these results would clearly result in the player providing a different value to the team.
In the table below, the decisions by the GM are listed on the left, in the rows. The possible resulting “states” of the situation are identified at the top of each column. The outcomes, which are combinations of the states and decisions, are the numeric values in the cells of the table and could represent surplus value (in millions of dollars) over the course of a rookie deal. The surplus value to the team is higher if they can draft GT in round 2 rather than round 1, since the team’s costs would be lower.
Note that we have made some simplifying assumptions here. First, we are assuming a running back viewed as a generational talent would only be available to draft in the first or second round. To keep the focus on the various approaches to decision making, we have also not incorporated probabilities that the player will be available when this team’s pick comes up in round 2. Also, if the team does not draft GT but has a need at running back, they would likely draft another player at this position later and get value from them. For simplicity’s sake here, we have recorded the value of not drafting GT as zero.
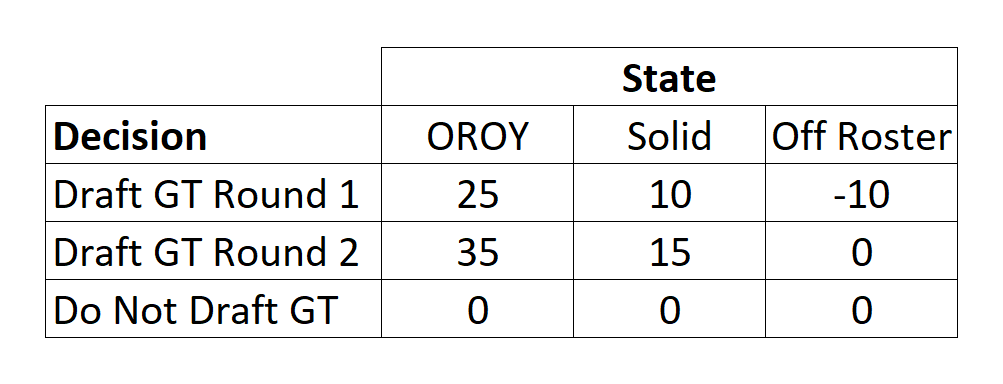
To use this criterion, the maximum across each row is found (25, 35, and 0), as indicated in the Maximax column below. Then, we select the maximum of these maxima, 35, and the suggested decision is to draft the GT running back in round 2, as indicated by the cells highlighted in green.
Maximin
The maximin (or “maximize the minimum”) approach, on the other hand, seeks to minimize the potential loss by selecting the option that offers the highest possible minimum payoff. This would involve selecting players who have a reliable performance history, assuming the worst possible outcome. In other words, a maximin decision aims for a higher floor. Decision makers using this approach would select players with what they deem to be a lower risk profile while prioritizing consistency and reliability over potential.
For example, a coach may choose an offensive lineman who demonstrates solid technique and maintains a healthy track record over one with extraordinary physical attributes but frequent injuries. Similarly, on defense, with its weak-link nature, a coach may prefer to maximize the worst player on the offensive line or among their defensive backs. This approach may be appropriate when the team or unit is risk-averse and is looking to avoid potential losses. The maximin approach is suitable for a GM looking to establish a baseline level of competitiveness.
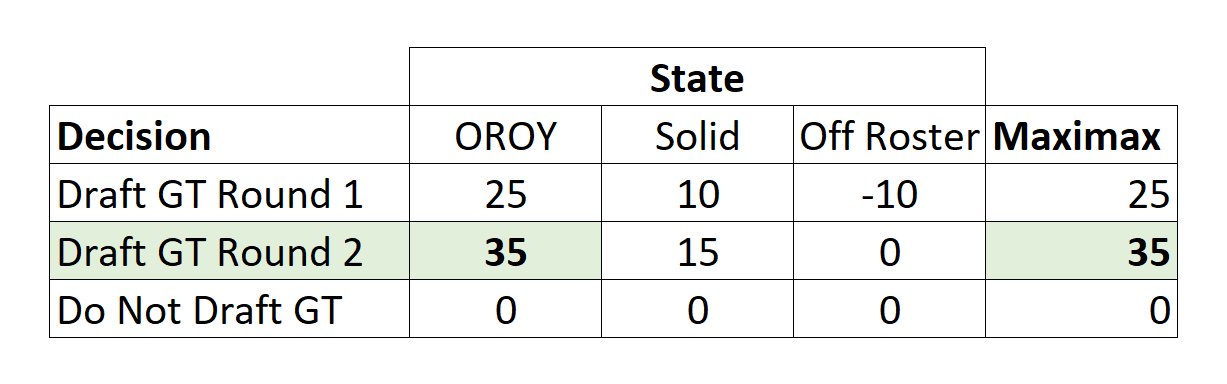
Here is a simple illustration of the maximin approach using our generational talent running back from above. The table is set up as before, but this time a different decision rule or criterion is being applied. First, the minimum of each row is found (and shown in the Maximin column). Then, the maximum of those minimums is chosen to suggest a decision. In this instance, there are two equivalent recommendations (drafting GT in round 2 and not drafting GT).
Minimax Regret
The minimax (or “minimize the maximum”) regret approach seeks to minimize the potential regret by selecting the option that offers the lowest possible maximum regret. This approach assumes that the decision maker will regret not selecting the option that would have performed the best in hindsight.
For example, a team may compare the regret of passing up on a wide receiver with great hands but questionable speed to the regret of not selecting a fast receiver with unreliable hands. On defense, a coach could weigh the regret of not selecting a defensive end with strong pass rush ability against the regret of not choosing a more balanced player with better run-stopping skills.
This approach may be appropriate when there is a high degree of uncertainty and no clear way to predict which players will perform best. The minimax regret approach is often used when the decision maker is unsure about the potential outcomes and wants to avoid making a decision that they will regret later. For example, think about a GM choosing between the following two players:
- An aging player who has produced well in the past but has a high salary cap number
- A young player who is on a cheap contract but is still unproven
The GM would ask, “Which of the following would I regret more: a decent (but not great) performance by someone using a relatively high percentage of the cap or a no-show by the young player who saved some money?” There does not appear to be a right answer here, but using the minimax regret might be helpful in framing the decision.
Here is a simple illustration of the minimax regret approach once again using our generationally talented running back. As before, the data is the same. However, the value of the outcome has been modified to represent “regret” in this instance.
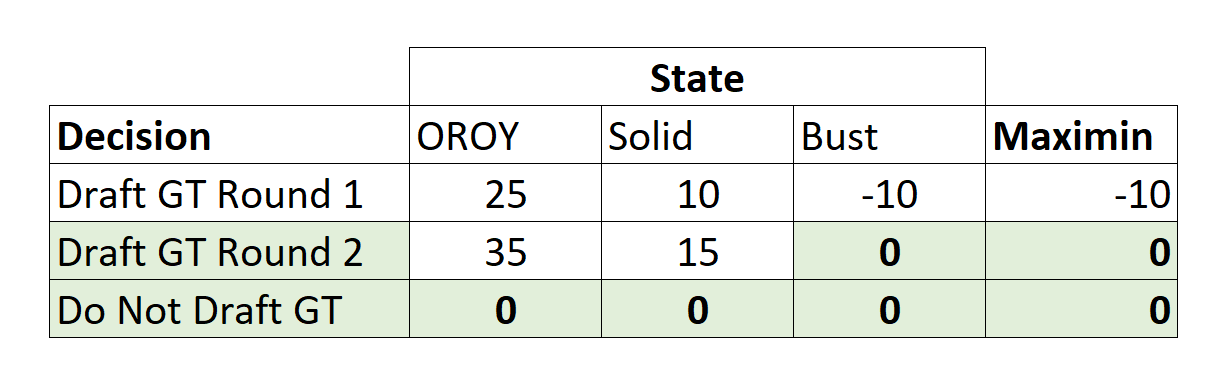
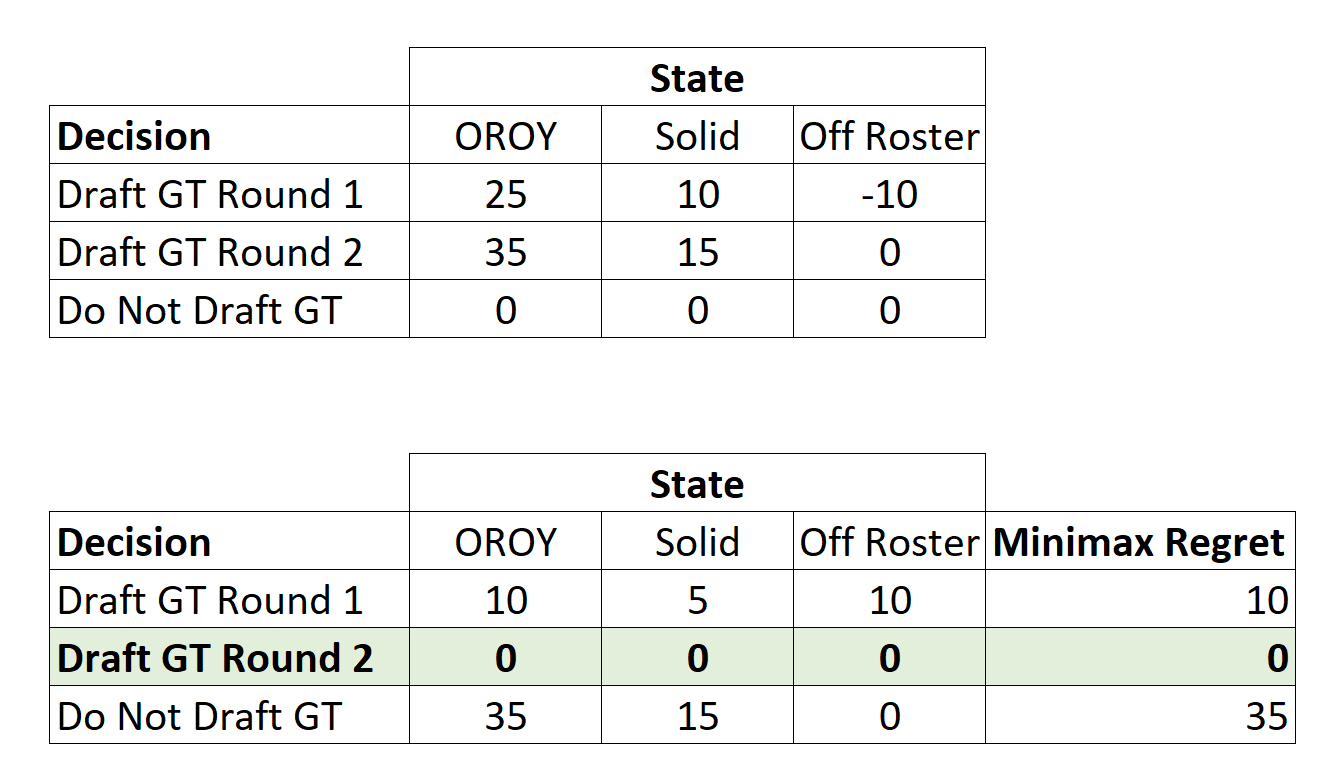
Using the payoffs in the first table below (a copy of the original value table presented), the regret amounts are calculated as follows. First, the maximum in each outcome or state is calculated. For the OROY column, it is 35. Then, regret is calculated by subtracting the payoff associated with each decision. Drafting GT in Round 1 has a regret amount of 35 – 25 = 10. Drafting GT Later has no regret since 35 – 35 = 0. Not drafting GT has the largest regret since 35 – 0 = 35. The process is then repeated for the other two columns. Then, the maximum regret is calculated for each decision (row), and the minimum of these is selected. In this example, since the regret associated with drafting GT in round 2 is 0, that is the suggested decision using this method.
Hurwicz Criterion
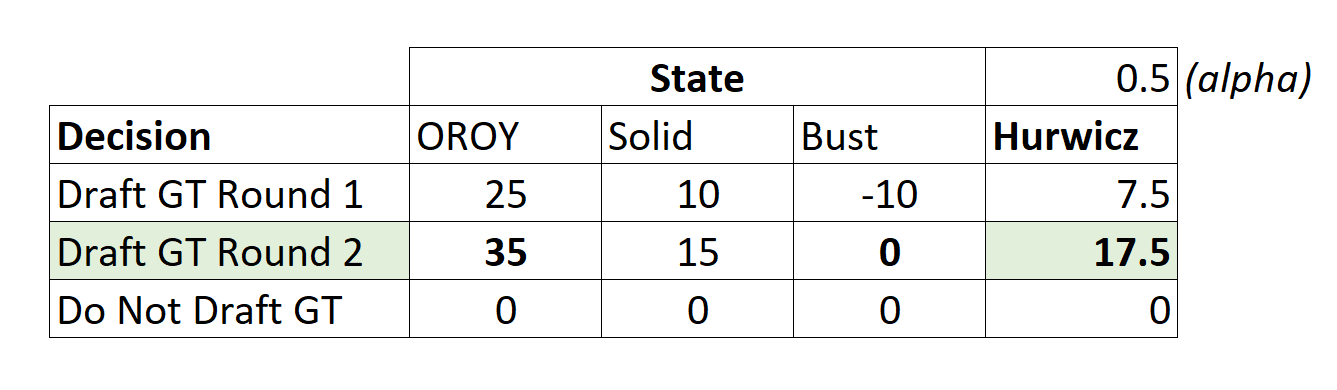
Finally, the Hurwicz Criterion is a weighted compromise between the maximax and maximin criteria. Payoffs are weighted using a “coefficient of optimism,” (alpha) between 0 and 1, which is a measure of the decision maker’s optimism regarding the outcome of events. Alpha is multiplied by the best payoff and (1-alpha) is multiplied by the worst payoff and the values are added together. This is a very subjective criterion but does start to take the decision maker’s risk preferences into account.
For example, using an alpha value of 0.5 (equally weighted between optimistic and pessimistic), the Hurwicz values are calculated by taking one-half the best outcome and adding one-half the worst outcome. For the first row (Draft GT in Round 1), this results in a value of (0.5)(20) + (0.5)(-5) = 7.5. Similar values are calculated for the remaining rows. Then, the largest value is selected. In this case, the recommended decision is once again to Draft GT in a round other than the first.
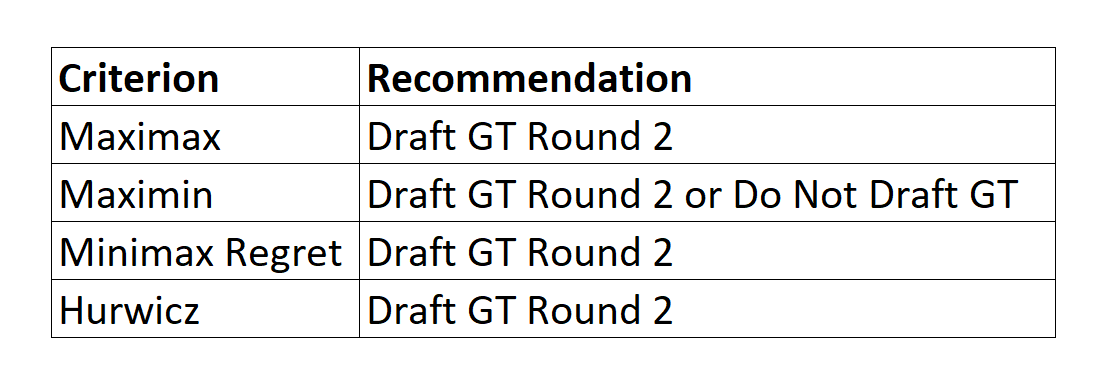
In the stylized example provided for the generational talent running back, each of these approaches suggested the same decision (drafting GT in the second round) except for the Maximin criterion, for which not drafting the player was also a recommended option. It is not always the case that the different criteria will suggest the same decision. At times, different approaches will suggest different decisions, and the decision maker must decide which approach is most in line with their view, considering the strengths and weaknesses of each approach.
In conclusion, adding players to a roster requires making decisions under uncertainty, which involves assessing multiple options and potential outcomes in situations where the future is uncertain. The maximax, maximin, minimax regret, and Hurwicz approaches are four different decision-making approaches that can be applied when selecting team members under such circumstances. Each approach caters to different risk tolerances and priorities, from the high-reward potential of the maximax approach to the reliability-focused maximin approach, while the minimax regret and Hurwicz criterion attempt to provide a balanced approach.
Team builders must carefully consider the trade-offs between these different approaches and select the approach, or combination of them, that is most appropriate for their team's goals and objectives. Ultimately, utilizing these methods in tandem (and with decision trees and probabilities of different outcomes) supports making good decisions and fielding a competitive team with a mix of talents and attributes.




